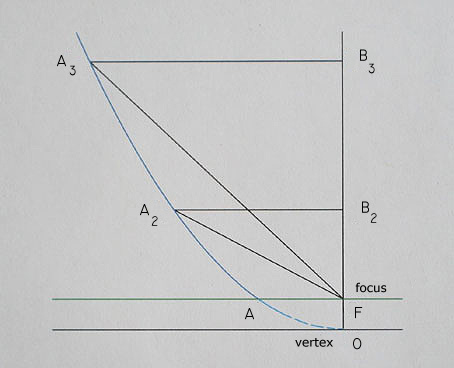

F is the focus of the parabola
O is the vertex of the parabola, at the intersection
of the x axis and the y axis
The x-length is measured, relative to F, along the lines BnAn, which are
straight lines parallel to the x axis. When the x-length is a constant, relative
to F, the endpoints of the segments form an x-length parallel curve, which is
part of a parabola. That part of the parabola between A and the vertex is considered
not to be a part of the x-length parallel curve.
The equation for the x-length parallel, from An to the point A, is the equation
for the parabola, between these points.
y = x²/2a x = (2ay)½
a is the x-length constant,
the focus of the parabola is (0,a/2)
in the diagram:
y = x2/8 is the equation of the parabola
a = 4
vertex = (0,0) focus = (0,2)
if the value of y at B3 is 8
the value of x at A3 is
x = [2(4)8]½
= (64)½
= 8