h-length of an oblique segment

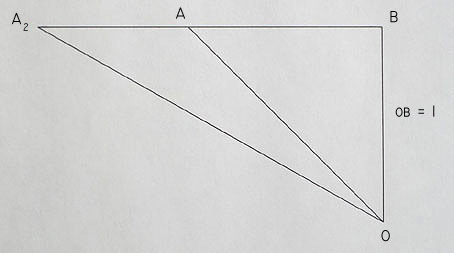
OB = 1
OA₂ = L₂
OA = L

The h-length of the segment A₂A, relative to O, equals the natural log of: L₂ divided by L.
L₂ equals L times: e raised to the power of the h-length
L equals L₂ times: e raised to the power of the negative h-length

h length = ln(L₂ / L)

L₂ = L(e^hlength )

L = L₂(e^-hlength )

in the diagram:
OA = L = 1.428571
OA₂ = L₂ = 2
OB = 1

h-length of A₂A, relative to O, is

h-length = ln(2/1.428571)
= .336472

the length of L₂ is

L₂ = 1.428571(e^.336472 )
= 1.428571(1.4)
= 2

the length of L is

L = 2(e^-.336472 )
= 2(.714285)
= 1.428571