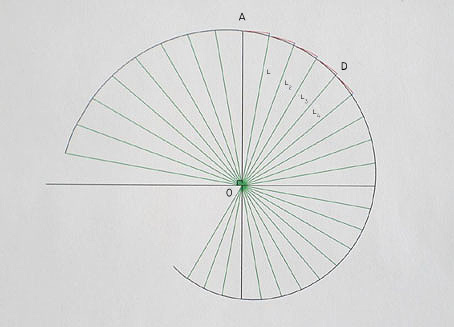

AO = 1
An approximation of the y-length of the spiral, from A to the
origin at O, is the sum of the red arcs. In the diagram, the
equation of the spiral is
L = e-aθ
(a = .1)
If the rays of the spiral are separated by .174532 radians (10 degrees),
then the first ray L equals
e-.1(.174532) = .982698
This is the common ratio between each ray Ln
The sum of the y-length approximations, from A to O:
= .174532 (1 + L + L2 + L3 + ....)
= .174532 (1 + L + L2 + L3 + ....)
= .174532 (1 / 1 - .982698)
= .174532 (57.7967)
= 10.087373
This amount is an approximation of the y-length of the log spiral from A
to the origin at O, relative to O.
If an approximation is calculated based on the rays being separated by 5
degrees, then the approximation improves to 10.043696.
If this process is continued ad infinitum, the approximation moves closer
and closer to being exactly 10.
In the example above, 1/a = 10, which is 1/a = y-length.
In a logarithmic spiral, the y-length from any point on the spiral to
the origin at O, relative to O, is the length of the ray (L) from that
point to the origin, divided by a.
L/a = y-length
The y-length between any two points on the spiral, relative to O, is the difference between the length of the two straight lines from the origin to those points, divided by a.
( L - Ln ) / a = y-length
in the diagram:
OD = .932568
a = .1
y-length from D to the origin at O, relative to O, is
.932568/.1
= 9.325675
y-length from A to D, relative to O, is
(1 - .932568) / .1
= .674325