y-length as part of a complex number (page 3)

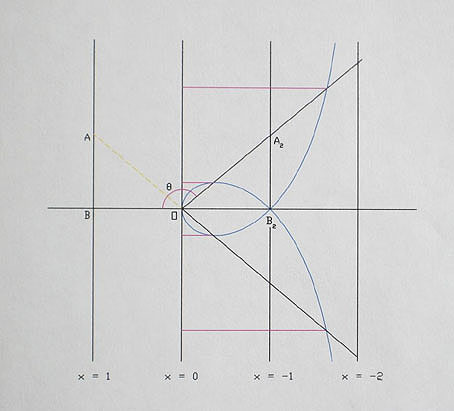
OB₂ = -1
the x-axis intersects the y-axis at O

If the angle used in the complex expressions are greater than π/2 (90°) then the sum of the four complex numbers they represent equals -4.

The y-length when θ = 2.443 (140°) equals the y-length of B₂A₂, relative to O. This could be interpreted as being the same as the y-length, relative to O, along the axis x = 1 from B to infinity, less the y-length along the axis x = -1 from infinity to the point A₂. This amount is the same as the y-length of BA, relative to O.

in the diagram, θ = .698131 (140°)
y-length = .762909