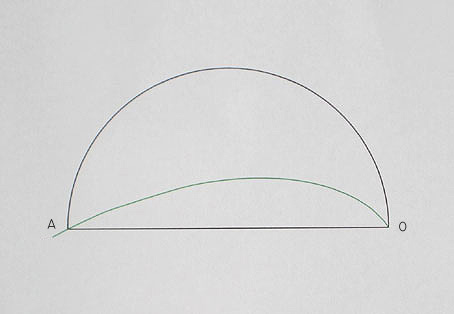

Measurements are taken along a straight line BA, which is perpendicular to
a unit line OB, as in the previous diagrams. At the scales involved in
the equalities below, this unit measurement is insignificant. The measurements
are referred to as being taken from O to A.
It should be noted that at the scales imagined, relative to the shape of the circle,
the logspiral would be indistinguishable from the straight line OA.
in the diagram,
the y-length of the circular arc OA, relative to O, equals the length of
the straight line OA.
As the arc length of the circle increases to a length that could be
imagined as approaching infinitely large, the y-length of that circle
from O to A, relative to O, could be thought of as representing unit
measurements of integers along the straight line from O to A.
Likewise, the y-length of the spiral from O to A, relative to O, multiplied
by 2/π represent the number of primes from O to A.
the approximate ratio of
#integers / #primes = y-length (of the circle) / y-length (of the spiral) 2/π
#integers/#primes = (π)y-length (of a circle) / (2)y-length (of a spiral)
The y-length of the arc of the circle, relative to O, being equal to the line OA, then that length multiplied by π/2 represents the arc length of the circle in the diagram.