equation for approx. #primes to large values of L

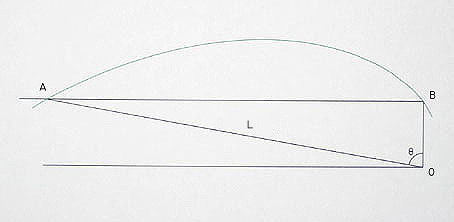
If the length L is considered to be increasing by unit measurements towards infinity at A, the angle at θ moves toward π/2, and (a), in the equation of the spiral passing through B and A (with its origin at O), moves toward being infinitely large.

approx. #primes = π(L) / 2(ln L) ArcTan(θ) SinArcTan(θ)

As (a) approaches becoming infinitely large ArcTan(θ) approaches π/2, and SinArcTan(θ) approaches 1, which leaves the equality in the Prime Number Theorom.

number of primes up to 10,000
when L = 10,000
θ = 89.9942° (1.570696 radians)

L = e^aθ

10,000 = e^a(1.570696)

a = 5.863858


approx. #primes = π(L) / 2(ln L) ArcTan(θ) SinArcTan(θ)

ArcTan(θ) = 1.401885
SinArcTan(θ) = .985768

approx. #primes = 31415.92654/25.45616496

= 1234.118595

rounded off, this amount is five primes above the exact number of 1229.

at L = 100,000 the equation gives an approx. of 9594 which is 2 primes above the exact amount.

at L = 1 million the approx. is 9 primes above the exact amount.

at 10 million the approx. is 124 primes less.

at L = 1 billion the approx. is 5468 primes less than the exact amount, which is .99989 accurate.

at L = 10¹¹, 10¹², 10¹³ the approximations are all above the exact amounts, being 1.000010191, 1.000037009, and 1.000051683 accurate.