e raised to the power of the sum of y-length plus h-length

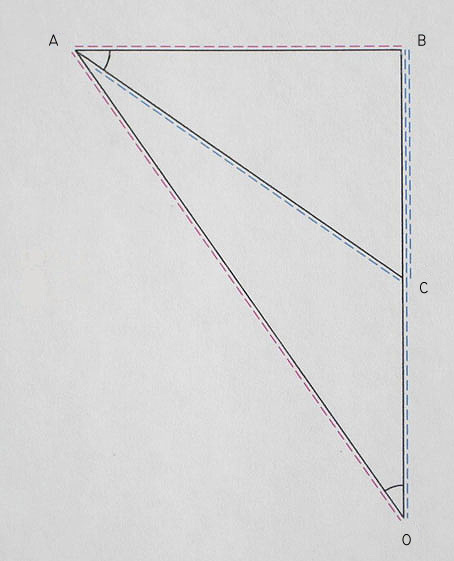
OB = 1
OA = L
BA = X
AB is perpendicular to OB
ABC and AOB are similiar triangles
angle CAB and AOB are equal

y-length of AB relative to O:
y-length = ln(L + X)
h-length of AB relative to O:
h-length = ln (L)

If the y-length and h-length are added together and used as exponent to the base e, that amount equals 1 + CB + CA.

e^{ylength + hlength} = 1 + CB + CA

in the diagram:
AB = .7
OA = 1.22065
OB = 1
CB = .49
AC = .854458

h-length, relative to O, is .199388
y-length, relative to O, is .652663

e^{.652663 + .199388} = 2.34445
= 1 + .49 + .854458
= 1 + CB + CA