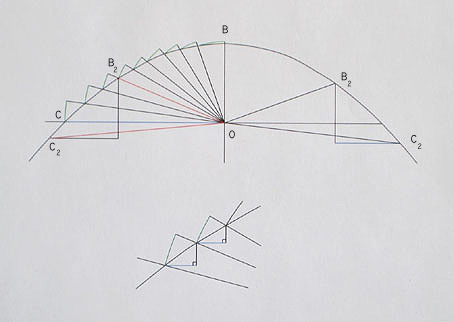

O is the focus of the parabola
B is the vertex of the parabola
The sum of the y-length segments, in green, are an approximation
of the y-length of a parabola from B to C, relative to O, which
is at the focus. As the segments are increased, ad infinitum, the
approximation becomes exact.
The length of the green arcs (y-length segments) are nearly equal
to the blue lines, which are straight line segments parallel to OC.
As the segments are increased, ad infinitum, the green lines approach
the blue lines in length. - The sum of the green lines represent the
y-length of BC, the sum of the blue lines equal the straight line OC.
- The y-length of BC, relative to O, equals the length of the line OC.
The y-length of a parabola from one point on the arc to another point,
relative to the focus, is equal to the difference in the x value of the
parabola between those points.
Perpendicular distance BC, relative to O.
y-length = (4y)½
= 2(y)½
Perpendicular distance B2C2, relative to O.
y-length = 2(y2)½ - 2(y)½
= 2[(y2)½ - (y)½
in the diagram:
OB = 4
OC = 8
x = 4(y)½ (equation of the parabola)
y-length of BC, relative to O, is
y-length = 4(4)½
= 8
y-length of B2C2, relative to O, is
y-length = 4(4.8334)½ - 4(1.7886)½
= 8.793998 - 5.349542
= 3.44445