prime numbers as they relate to the y-length of a logspiral

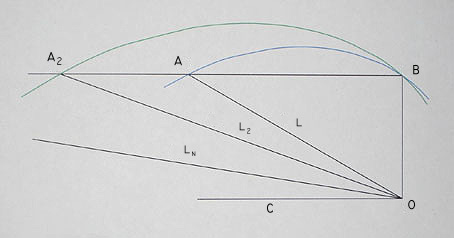
OB = 1
OB is perpendicular to the straight lines
passing through OC and BA₂

The arcs A₂B and AB are segments of log spirals
with their origins at O.

angle AOB = 60° (1.047197 rad.) L = 2
angle A₂OB = 70° (1.22173 rad.) L₂ = 2.9238

The equation of a logarithmic spiral being L = e^aθ, the value of (a) in the equation of the spiral passing through the points B and A is

2 = e^a(1.0471)
a = .6619

The value of (a) in the equation of the spiral passing through
the points B and A₂ is

2.9238 = e^a(1.2217)
a = .8781


As the value of the angle A₂OB approaches π/2, the length of the line L_n increases, intersecting the straight line passing through BA at a point A_n. The expression below is a good approximation for extremely large values L_n. As the length of L_n approaches infinity, the expression below is virtually exact.

ln L_n = (a)π/2

Likewise, the expression below for prime numbers, n representing the domain of whole numbers for large values of n.

ln n = n/#primes