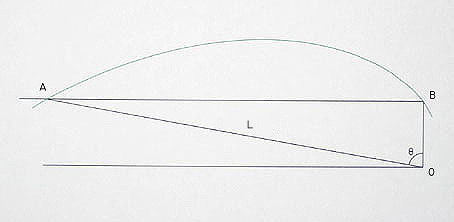

OB = 1
The whole numbers being conceived as representing units of length on
the line L, then the equalities below are virtually correct
for extremely large values of L.
The x-length and y-length values are those of the log spiral,
measured relative to O.
n/#primes = L/#primes
ln n = L/#primes
L/#primes = (a)π/2
#primes = 2L/π(a)
(a) being x-length/y-length, then
#primes = 2L/π(x-length/y-length)
#primes = 2(L)y-length/(π)x-length
L being extremely large, then L and x-length could be considered
equal, and cancel out of the equation.
#primes = 2(y-length)/π
As the value of (a) in the equation of the log spiral increases, L
approaches being an infinitely large number, and the value of θ
approaches π/2. It should be noted however, how slowly the value of (a)
increases relative to L. When L is 10 billion, the value of (a) in
the equation of the corresponding spiral is 14.658.
The y-length in the equation is defined as being the perpendicular
distance of the log spiral relative to O, from B to A. Considering
the extreme length of L, the y-length could reasonably be conceived
as being taken from A to the origin at O, the y-length from O to B,
relative to O, being negligible.