Euler's constant as the difference between dimensions of h-length

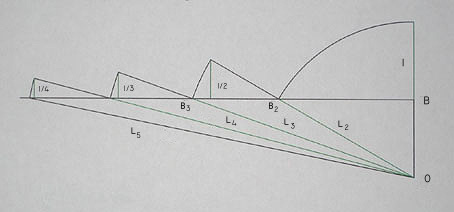
OB = 1
L₂ = 2,  L₃ = 3,  etc.

If OB and the diagonals L₂, L₃, L₄.... L_n form the arithmetic progression 1, 2, 3, 4, .... n, the corresponding h-length segments represent the harmonic series 1, 1/L₂, 1/L₃ ..... 1/L_n. As n approaches infinitely large, the sum of these vertical segments represent the sum of the harmonic series.

An approximation of each term can be made by taking the h-length between corresponding diagonals along the line BA, relative to O. e.g. The vertical segment 1/2, being the reciprocal of L₂, can be approximated by taking the h-length of the segment B₃B₂, relative to O.

ln 3 - ln 2 = ln 3/2 = .405465

The approximation of any vertical segment which is a term in the harmonic series, can be expressed as

ln (L_n + 1) / L_n = approx. of the harmonic term

As n becomes larger the approximation becomes more exact.
As n becomes infinitely large, the difference between the h-length of the line up to B_n and the sum of the harmonic series up to that same point, approaches the value of Euler's constant (.577218). This constant could be thought of as the difference between the h-length of BA, as L_n approaches infinitely large, and the sum of those segments of h-length represented when the diagonals are increasing by an arithmetic progression of one. (i.e. the harmonic series)