y-length complex spiral (page 3)

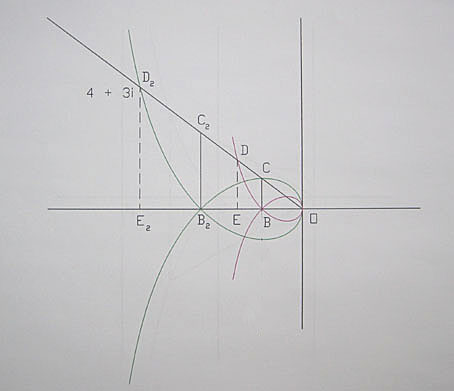
OC = 1.25
BC = .75
OB = 1

Cosθ = .8
Sinθ = .6
Tanθ = .75

A point on the complex plane is contained by only one complex spiral. Consider the location of the complex number at D, contained by the complex spiral with the base OB = 1. The length OE is defined by the equation below.

OD = e^ylength(Cosθ)

as e^ylength equals BC + OC, then

OD = 2

OE = 2Cosθ = 1.6


The length OB₂ represents the length of the base which contains the point 4 + 3i.
The two spirals being proportional to each other, then

OE/OB = OE₂/OB₂

The length OB being equal to 1, then

OE/1 = OE₂/OB₂

OB₂ = OE₂/OE = OE₂/[(Tanθ + 1/Cosθ)]Cosθ

= OE₂/[Sinθ + 1]


Given the complex number x + yi, the base of the spiral which contains this number is calculated by the formulas below.

base = x/[1 + Sinθ]

if y > 0

base = y/[Tanθ(1 + Sinθ)]

given the complex number 4 + 3i, then

base = 4/[1 + .6]
= 2.5


base = 3/[.75(1 + .6)]
= 2.5